polyèdre

polyèdre [ pɔljɛdr; pɔliɛdr ] n. m. et adj.

• 1690; gr. poluedros; cf. poly- et -èdre

♦ Géom. Solide limité par un nombre fini de polygones plans ou faces. Polyèdre convexe. Polyèdre régulier. ⇒ cube, parallélépipède, pyramide. Polyèdre (concave) à faces étoilées. — Adj. Angle polyèdre, formé par les faces d'un polyèdre.

● polyèdre adjectif (grec poluedros, à plusieurs faces) Angle polyèdre ou secteur polyèdre, portion illimitée d'espace dont la frontière est la réunion de parties planes, celles-ci (faces) étant des secteurs angulaires (dont les côtés sont les arêtes du secteur polyèdre) de même sommet, appelé sommet du secteur polyèdre. ● polyèdre (expressions) adjectif (grec poluedros, à plusieurs faces) Angle polyèdre ou secteur polyèdre, portion illimitée d'espace dont la frontière est la réunion de parties planes, celles-ci (faces) étant des secteurs angulaires (dont les côtés sont les arêtes du secteur polyèdre) de même sommet, appelé sommet du secteur polyèdre. ● polyèdre nom masculin Solide de l'espace de dimension 3 dont la frontière est réunion de parties de plans. (Ces parties sont les faces, leurs côtés communs sont les arêtes, dont les points communs sont les sommets du polyèdre.) Frontière de ce solide.

polyèdre

n. m. et adj. GEOM Solide dont les faces sont des polygones.

— Polyèdre régulier, dont les faces sont des polygones réguliers égaux.

— Polyèdre convexe, dont l'une quelconque des faces, prolongée indéfiniment, laisse toute la figure du même côté.

|| adj. Angle polyèdre (ou angle solide): figure formée, dans un polyèdre, par les faces et les arêtes qui ont un sommet commun.

⇒POLYÈDRE, subst. masc. et adj.

GÉOMÉTRIE

I.— Subst. masc. Solide délimité par des faces polygonales dont les intersections forment des arêtes et les points de rencontre de celles-ci, des sommets. Pour faciliter aux voyageurs la recherche de ces variétés [de minéraux], l'académie leur fera remettre des polyèdres exécutés en bois, qui en représentent exactement les formes (Voy. La Pérouse, t. 1, 1797, p. 170) :

• Soit, par exemple, cette proposition de géométrie : « Le nombre des angles solides d'un polyèdre, ajouté au nombre de ses faces, donne une somme supérieure de deux unités au nombre de ses arêtes » : on pourra construire autant de polyèdres qu'on voudra, et l'on trouvera toujours que le théorème se vérifie en toute rigueur...

COURNOT, Fond. connaiss., 1851, p. 482.

♦ Polyèdre convexe. Polyèdre situé tout entier du même côté du plan de chacune de ses faces. Anton. polyèdre étoilé, à faces étoilées. La recherche d'un sommet sur un polyèdre convexe, représentant l'ensemble des solutions possibles (Hist. gén. sc., t. 3, vol. 2, 1964, p. 119). En 1809, Poinsot a découvert les polyèdres réguliers étoilés qui diffèrent des polygones réguliers ordinaires en ce qu'ils ne sont pas convexes (QUILLET 1965).

♦ Polyèdre régulier. Polyèdre dont toutes les faces sont des polygones réguliers égaux et dont tous les angles dièdres ou polyèdres sont égaux. Anton. polyèdre irrégulier. Il existe seulement cinq polyèdres réguliers, dont le nombre des faces ne peut être égal qu'à l'un des cinq nombres entiers : 4, 6, 8, 12, 20 (E. BOREL, Paradoxes de l'infini, 1946, p. 19). Les cinq types de polyèdres réguliers sont : (...) Le tétraèdre régulier (...) Le cube (...). L'octaèdre régulier (...) Le dodécaèdre régulier (...) L'icosaèdre régulier (UV.-CHAPMAN 1956). Les polyèdres irréguliers sont le prisme et la pyramide (BÉG. Dessin 1978).

II.— Adj. Qui a la forme d'un polyèdre; qui fait partie d'un polyèdre. Synon. polyèdre (infra dér.). Corps polyèdre. Les solides bruts ne se composent que de molécules polyèdres qui s'attirent par leurs facettes et ne s'écartent que pour se séparer (CUVIER, Anat. comp., t. 1, 1805, p. 9).

♦ Angle polyèdre. Dans un polyèdre, figure formée par une suite fermée de faces ayant un même sommet. Angle polyèdre à trois faces (BOUVIER-GEORGE Math. 1979).

REM. Polyédriste, subst., rare, beaux-arts. Peintre représentant d'une tendance du cubisme. Nous avons vu, surtout après la guerre, les curiosités ou approximations cubistes. Bien rares sont aujourd'hui les tenants de cette école de tout repos, à laquelle fit suite celle des polyédristes, aussi désuète aujourd'hui que la précédente (L. DAUDET, Idées esthét., 1939, p. 36).

Prononc. et Orth. :[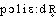], []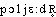. Pt ROB., WARN. 1968, les 2 prononc.; Lar. Lang. fr. [-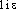-]; MARTINET-WALTER 1973 [-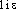-] (12/ 17), [-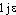-] (5/17). Att. ds Ac. dep. 1762. Étymol. et Hist. 1690 polièdre subst. « corps solide qui a plusieurs faces » (FUR.); 1690 adj. lunettes polièdres (ibid.); 1845 angle polyèdre (BESCH., s.v. angle). Comp. des élém. poly- et -èdre sur le modèle du gr. 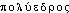« à plusieurs sièges ou degrés », comp. de 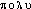- élém. 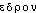tiré de « nombreux » et de - subst. au neutre des adj. en -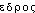, de 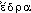« place siège, base ». Fréq. abs. littér. :20.

DÉR. Polyédrique, adj. a) Qui a la forme d'un polyèdre; qui constitue un polyèdre. Figures polyédriques. Les monuments de blocs polyédriques qu'on rencontre en Grèce, en Italie, en France et jusqu'au fond de l'Espagne (FULCANELLI, Demeures philosophales, t. 1, 1929, p. 113). La ferrite se présente sous la forme de grains polyédriques (BARNERIAS, Aciéries, 1934, p. 16). b) Beaux-arts. Qui est constitué de polyèdres. Le cubisme apparaît en 1908. Braque en est l'initiateur avec les paysages de Provence (1907), de la Roche-Guyon (1909) stylisés et déjà en partie polyédriques (Arts et litt., 1936, p. 18-10). — [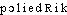], [-lje-]. — 1^re attest. 1832 figure polyédrique (RAYMOND); de polyèdre, suff. -ique.

polyèdre [pɔljɛdʀ; pɔliɛdʀ] n. m.

ÉTYM. 1690; grec poluedros. → -èdre.

❖

1 N. m. Géom. Solide limité de toutes parts par des polygones plans (⇒ Face, facette. → Édifice, cit. 1). || Polyèdre convexe. || Polyèdre régulier, irrégulier. || Polyèdres réguliers convexes : tétraèdre, hexaèdre (cube), octaèdre, dodécaèdre icosaèdre. || Polyèdre (concave) à faces étoilées.

♦ Allus. littér. || Les Polyèdres, titre initial probable de Ubu cocu, de Jarry (cf. Michel Arrivé, in A. Jarry, Œ. compl., Pl.).

0 Ô mais c'est que, voyez-vous bien, je n'ai point sujet d'être mécontent de mes polyèdres; ils font des petits toutes les six semaines, c'est pire que des lapins. Et il est bien vrai de dire que les Polyèdres réguliers sont les plus fidèles et les plus attachés à leur maître, sauf que l'Icosaèdre s'est révolté ce matin et que j'ai été forcé, voyez-vous bien, de lui flanquer une gifle sur chacune de ses faces.

A. Jarry, Ubu cocu, II, Œ. compl., Pl., t. I, p. 496.

2 Adj. || Angle polyèdre (concave, convexe). || Corps polyèdre.

❖

DÉR. Polyédrique.

Encyclopédie Universelle. 2012.